Official Website Universitas Ma Chung.
T : (0341) 550 171
Email: [email protected]
Universitas Ma Chung
Villa Puncak Tidar N-01, 65151, Malang, IND
Mengolah Citra Digital Melalui Transformasi Fourier (Bagian 1)
Penulis: Windra Swastika, Ph.D
Transformasi Fourier memungkinkan kita untuk memandang citra digital melalui dimensi yang lain, yaitu dimensi frekuensi. Tapi, so what?
Bagi sebagian besar mahasiswa teknik (elektronika atau informatika) yang mengambil mata kuliah Aljabar Linier, Metode Numerik, Pengolahan Citra Digital, atau Pengolahan Sinyal Digital, kemungkinan besar akan bertemu dengan materi Fourier Transformation atau Transformasi Fourier. Berusaha memahami Transformasi Fourier dari buku teks atau penjelasan dosen (yang sangat terbatas jam tatap mukanya), mungkin malah membuat filosofi dasar dari Transformasi Fourier menjadi semakin sulit dipahami. Seringkali kesulitan muncul pada perhitungan Transformasi Fourier yang melibatkan fungsi trigonometri, eksponensial, dan integral. Pada akhirnya, banyak mahasiswa yang fokus pada bagaimana menyelesaikan soal (agar bisa dapat nilai baik di ujian), tanpa peduli dengan filosofi dasar serta bagaimana menerapkan Transformasi Fourier dalam suatu aplikasi yang nyata.
Citra Digital Sebagai Sebuah Sinyal
Sebelum melangkah lebih jauh tentang Transformasi Fourier (yang akan diterapkan terhadap sinyal), mungkin banyak pembaca yang lebih familiar dengan istilah citra digital (digital image) ketimbang sinyal (signal). Keep in mind bahwa suatu citra digital (dalam format apapun, JPEG, BMP, TIF dan sebagainya) dapat dipandang sebagai sebuah sinyal.
Mengapa mengolah sinyal begitu penting? Dalam kehidupan sehari-hari, sadar atau tidak sadar, kita seringkali bertemu dengan sinyal. Beberapa contoh sinyal yang sering kita jumpai (walaupun secara visual tidak nampak) misalnya, sinyal ponsel, radio, televisi, suara yang kita keluarkan, detak jantung, gerakan partikel (dan citra digital yang juga dapat disebut sebagai sinyal). Intinya, segala macam bentuk yang dapat diukur energinya yang terjadi dalam suatu waktu atau ruang dapat dipandang sebagai sinyal. Pada suatu citra digital, yang disebut energi adalah intensitas warna kelabu (pada citra grayscale) dan red/green/blue (pada citra berwarna). Sementara yang disebut ruang adalah sistem koordinat 2 dimensi pada suatu citra. Dengan cara demikian, suatu citra dapat dipandang sebagai sinyal sehingga berlaku Tranformasi Fourier beserta segala propertinya.
Dalam keadaan di mana sinyal masih berada dalam kawasan waktu (atau ruang), pengolahan yang dapat dilakukan akan terbatas. Namun ketika sinyal tersebut ditransformasi ke dalam kawasan frekuensi, maka pengolahan terhadap sinyal tersebut menjadi lebih praktis. Misalnya, (setelah sinyal berada dalam kawasan frekuensi) dapat dilakukan penapisan (filtering) untuk mengurangi derau (noise) pada sinyal (baik pada sinyal berupa suara ataupun pada citra digital). Transformasi Fourier merupakan sebuah metode atau kakas (tool) untuk mengubah suatu sinyal dalam kawasan waktu menjadi kawasan frekuensi. Setelah sinyal berada dalam kawasan frekuensi dan diolah, sinyal dapat dikembalikan menjadi kawasan waktu kembali.
Mengapa Ada Transformasi Fourier?
Tranformasi Fourier diawali di abad ke-19 (tepatnya tahun 1822) oleh seorang matematikawan Perancis yang bernama Jean Baptiste Fourier. Dalam penelitiannya, Fourier berhasil menunjukkan bahwa semua fungsi yang bersifat periodik (sinyal) dalam waktu dapat diekspresikan sebagai fungsi penjumlahan (integral) trigonometri sinus dan cosinus dari berbagai frekuensi. Tidak peduli bagaimana rumitnya bentuk dari sebuah sinyal, selama sinyal tersebut periodik dan memenuhi beberapa kondisi matematika, maka sinyal tersebut akan dapat direpresentasikan dalam penjumlahan fungsi sinus dan cosinus. Sebagai contoh, diketahui bentuk dari sinyal x dalam fungsi waktu adalah seperti pada gambar 1.
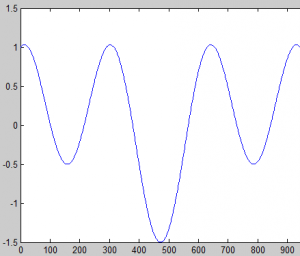
Berdasarkan teori yang dipaparkan Fourier, sinyal tersebut dapat digambarkan sebagai fungsi penjumlahan dari sinus dan cosinus, yaitu f(t)=1/2 sin (t)+cos(2t), di mana t merupakan periode (waktu).
Secara umum, representasi Deret Fourier dari sebuah sinyal didefinisikan dengan rumus 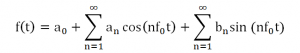
di mana a0, an, dan bn merupakan koefisien dari deret Fourier. Dengan menggunakan rumus tersebut, untuk bentuk sinyal yang rumit seperti square signal (sinyal ini muncul pada berbagai perangkat elektronik digital) juga dapat didekati sebagai fungsi penjumlahan dari fungsi sinus dan cosinus.
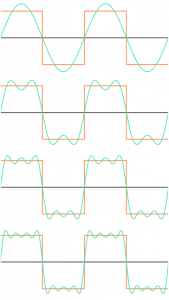
Pada gambar 3 di atas, baris pertama merupakan contoh pendekatan square signal dengan menggunakan fungsi sinus biasa. Pada baris berikutnya, didekati dengan fungsi sin(t) + 1/3 sin(3t), baris berikutnya didekati dengan fungsi sin(t)+1/3 sin(3t)+1/5 sin(5t) dan seterusnya. Semakin banyak penjumlahan yang dilakukan, maka pendekatan akan semakin baik.
Secara umum, bentuk pendekatan dari sinyal tersebut dengan menggunakan Deret Fourier adalah
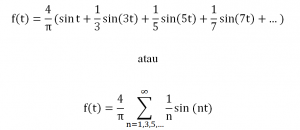
Setelah fungsi dari sebuah sinyal dapat didefinisikan dalam kawasan waktu, maka sinyal fungsi tersebut dapat diubah ke dalam kawasan frekuensi. Seperti yang disinggung pada bagian sebelumnya, pengubahan kawasan sinyal dari waktu menjadi frekuensi menjadikan sinyal lebih mudah dianalisa ataupun diolah. Sekedar gambaran misalkan pada saat komputer memainkan file musik berformat MP3. Jika software untuk memainkan musik dilengkapi dengan spectrum analyzer, maka akan nampak berbagai frekuensi yang muncul saat musik dimainkan. Dari berbagai frekuensi tersebut, dapat dideteksi mana bass, treble, vokal dan sebagainya. Dengan mengolah sinyal pada kawasan frekuensi seperti ini, dapat dilakukan pengolahan seperti menghilangkan frekuensi tertentu (yang merupakan noise) sehingga menghasilkan musik yang lebih jernih. Hal ini akan sulit dilakukan jika sinyal masih berada dalam kawasan waktu.
Fourier mendefinisikan transformasi sinyal dari kawasan waktu ke kawasan frekuensi dengan rumus:
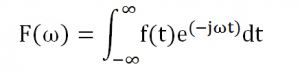
Sebaliknya, untuk mengubah sinyal dari kawasan frekuensi menjadi kawasan waktu (melakukan invers) dengan menggunakan rumus:
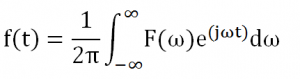
F(w) merupakan spektrum, di mana w mewakili frekuensi, dan f(t) merupakan sinyal asli dalam kawasan waktu. Bilangan j yang muncul adalah bilangan kompleks (akar -1). Batas atas dan batas bawah dari integral adalah plus minus tak terhingga, yang menyatakan bahwa sinyal tersebut merupakan sinyal kontinyu (periodik) dari rentang minus tak terhingga sampai plus tak terhingga.
Sinyal dalam rentang tersebut, akan sulit diolah oleh komputer. Untuk itu, sinyal perlu didiskritkan dan diberikan batas dalam waktu tertentu (atau istilahnya dilakukan sampling). Pada sebuah file musik digital sekualitas CD, sampling yang dilakukan adalah 44.100 sampling per detik. Artinya dalam satu detik, ada 44.100 data yang dicuplik. Pada kasus musik digital, semakin tinggi nilai sampling, tentu kualitas suara yang dihasilkan akan lebih baik.
Jika sinyal telah menjadi sinyal yang diskrit, maka batas atas dan batas bawah dari integral dapat dibatasi dan diubah dalam bentuk penjumlahan biasa. Proses transformasi Fourier untuk sinyal yang telah menjadi diskrit (mempunyai batas yang tertentu) disebut sebagai Discrete Fourier Transform (DFT). Rumus untuk DFT adalah sebagai berikut:
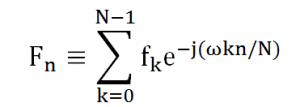
Untuk mengembalikan menjadi sinyal dalam kawasan waktu, rumus DFT yang digunakan adalah:
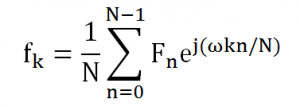
Transformasi Fourier Untuk 1D
Sebelum kita masuk pada Transformasi Fourier untuk citra (2D), kita perlu memahami bagaimana konsep Transformasi Fourier untuk sinyal 1 dimensi. Inti dari Transformasi Fourier adalah mengubah sinyal dalam kawasan waktu ke dalam kawasan frekuensi. Dengan men-transformasi sinyal ke dalam kawasan frekuensi, kita dapat melihat frekuensi berapa sajakah yang muncul pada sinyal tersebut.
Bahasa Pemrograman Java atau C++ dapat digunakan untuk mensimulasikan bagaimana Transformasi Fourier dilakukan. Namun untuk mempermudah proses coding, kita akan menggunakan software Matlab. Pada Matlab, fungsi-fungsi untuk melakukan plotting grafik serta melakukan transformasi Fourier telah disediakan sehingga tidak repot melakukan coding.
Script Matlab berikut akan menghasilkan grafik yang mewakili sebuah sinyal yang dicuplik 100 sample per detik dengan durasi selama 3 detik. Pada fungsi sinyal, diberikan komponen frekuensi sebesar 10Hz dan 15Hz dengan ditambahkan nilai acak.
fs=100; % sampling 100 cuplikan/detik
duration=3; % selama 3 detik
t = 0:1/fs:duration-1/fs;
x = 1.3*sin(2*pi*10*t) ... % 10 Hz component
+ 1.7*sin(2*pi*15*t)... % 15 Hz component
+ 1.5*randn(size(t)); % penambahan derau (noise)
subplot(2,1,1), plot(t,x);
n = 512;
y = fft(x,n); % DFT
f = (0:n-1)*(fs/n); % Frequency range
ab = abs(y); % Nilai absolute
subplot(2,1,2), plot(f, ab);
xlabel('Frequency (Hz)');
Untuk mengubah suatu sinyal dalam kawasan waktu ke dalam kawasan frekuensi pada Matlab menggunakan Fast Fourier Transform, fungsi yang digunakan adalah fungsi fft. Fungsi ini mempunyai 2 parameter, yaitu x yang menunjukkan sinyal yang hendak ditransformasi dan n yang merupakan panjang sinyal dalam 2x. Pada contoh di atas, karena terdapat 100 sampling per detik dan dilakukan selama 3 detik, maka total panjang sinyal (jumlah total sampling) adalah 300. Panjang sinyal untuk proses FFT yang dibutuhkan adalah 29 atau 512 (2 pangkat sekian yang paling mendekati 300).
Nilai hasil Transformasi Fourier dengan menggunakan fungsi FFT (pada variabel y) mengandung bilangan kompleks (akar minus 1) yang tidak dapat diplotting. Untuk itu, hasil dari FFT di-absolute-kan dengan fungsi abs agar bisa diplot dalam grafik.
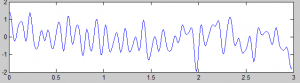
Hasil plotting sinyal dengan komponen frekuensi 10Hz dan 15Hz dalam kawasan waktu seperti pada gambar berikut.
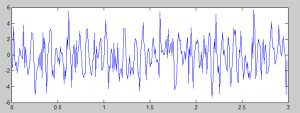
Transformasi Fourier dalam kawasan frekuensi untuk sinyal di atas adalah sebagai berikut:
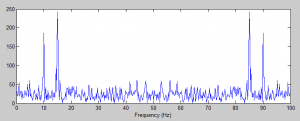
Pada gambar di atas, sumbu x mewakili frekuensi yang muncul pada sinyal. Nampak pada frekuensi 10 dan 15, terdapat puncak (peak) yang lebih tinggi dari nilai lain. Ini menunjukkan bahwa pada sinyal mengandung kedua frekuensi tersebut. Kedua puncak yang muncul di akhir sebenarnya hanya merupakan refleksi dari kedua puncak pada frekuensi 10Hz dan 15Hz, sementara puncak-puncak yang lebih rendah di frekuensi lainnya dihasilkan dari derau (noise) yang ditambahkan pada sinyal.
Dari visualisasi kawasan frekuensi tersebut, kita dengan mudah melakukan pengolahan, seperti melakukan penapisan (filtering) untuk menghapus frekuensi tertentu (tinggi, menengah atau rendah) yang muncul pada sinyal tersebut. Sebagai contoh, misalkan kita akan menghapus frekuensi tinggi yang muncul pada sinyal tersebut. Yang dibutuhkan adalah sebuah saringan (mask) yang bisa melewatkan frekuensi rendah dan meng-nol-kan frekuensi tinggi. Skrip berikut digunakan untuk membuat saringan, melakukan penapisan pada sinyal kawasan frekuensi hasil Fourier Transform, kemudian dari hasil penapisan, sinyal dikembalikan pada kawasan waktu. Hasil sinyal pada kawasan waktu menunjukkan hilangnya komponen pada frekuensi tinggi.
Skrip untuk mendapatkan saringan (mask) yang dapat melewatkan frekuensi rendah dan menghapus frekuensi tinggi.
mask = zeros(1, n); l = 0:n/2; sigmaf = 10; mask(1:n/2+1) = exp(-(l/(5*sigmaf)).^2); mask(n:-1:n/2+2) = mask(2:n/2); subplot(3,1,1); plot(f,mask);
Saringan tersebut akan dikalikan terhadap sinyal pada kawasan frekuensi. Hasil dari perkalian ini adalah sinyal-sinyal pada frekuensi rendah, sementara sinyal pada frekuensi tinggi telah hilang (0).
Xfilt = y .* mask; subplot(3,1,2); plot(f,abs(Xfilt));
Bentuk sinyal setelah disaring adalah seperti pada gambar berikut:
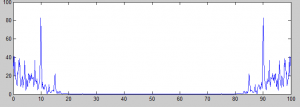
Sinyal di atas adalah sinyal dalam kawasan frekuensi. Untuk menjadi sinyal dalam kawasan waktu, yang perlu dilakukan adalah melakukan invers Transformasi Fourier. Fungsi yang digunakan untuk mengembalikan sinyal dari kawasan frekuensi menjadi kawasan waktu adalah fungsi ifft. Skrip yang digunakan untuk mengubah menjadi kawasan waktu kemudian melakukan plot adalah sebagai berikut:
xfilt = ifft(Xfilt); xfilt2 = xfilt(1:300); plot(t,xfilt2);
Pada skrip di atas, xfilt merupakan hasil invers untuk Xfilt (sinyal di kawasan frekuensi sepanjang 512). Agar dikembalikan menjadi sinyal asli sepanjang 3 detik dan tiap detik 100 cuplikan, maka hanya perlu diambil dari data ke-1 sampai dengan data ke-300. Sinyal dalam kawasan waktu dapat dilihat pada gambar berikut. Sinyal tersebut telah bersih dari komponen frekuensi tinggi.
Penutup
Pada bagian ini, dibahas tentang bagaimana konsep Transformasi Fourier pada sinyal 1 dimensi serta penerapannya untuk menghapus frekuensi tinggi melalui proses penapisan. Mungkin pada tahap ini, bagaimana penerapan Transformasi Fourier secara nyata masih belum begitu nampak. Pembahasan Transformasi Fourier pada 1 dimensi diperlukan sebagai fondasi untuk pembahasan berikutnya, yaitu Transformasi Fourier 2 dimensi.